
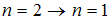
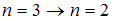
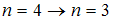
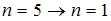
 ЗАДАНИЕ N 1
сообщить об ошибке
ЗАДАНИЕ N 1
сообщить об ошибке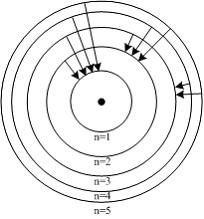

| 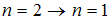 | ||
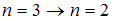 | |||
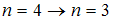 | |||
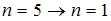 |
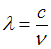 . Поэтому наибольшей длине волны (а следовательно, наименьшей частоте) кванта в серии Лаймана соответствует переход
. Поэтому наибольшей длине волны (а следовательно, наименьшей частоте) кванта в серии Лаймана соответствует переход 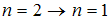 .
. ЗАДАНИЕ N 2
сообщить об ошибке
ЗАДАНИЕ N 2
сообщить об ошибке

| 16 | ||
| 100 | |||
| 32 | |||
| 8 |
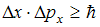 следует, что
следует, что 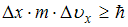 . Здесь
. Здесь 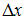 – неопределенность координаты,
– неопределенность координаты, 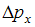 – неопределенность x-компоненты импульса,
– неопределенность x-компоненты импульса, 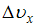 – неопределенность x-компоненты скорости,
– неопределенность x-компоненты скорости, 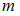 – масса частицы;
– масса частицы; 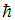 – постоянная Планка, деленная на
– постоянная Планка, деленная на 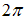 . По условию
. По условию 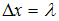 , где
, где 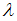 – длина волны де Бройля, определяемая соотношением
– длина волны де Бройля, определяемая соотношением 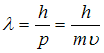 . Здесь
. Здесь 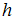 – постоянная Планка. Подставляя это выражение в соотношение неопределенностей, получаем:
– постоянная Планка. Подставляя это выражение в соотношение неопределенностей, получаем: 
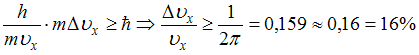 .
. ЗАДАНИЕ N 3
сообщить об ошибке
ЗАДАНИЕ N 3
сообщить об ошибке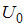 и ширины
и ширины 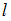 .
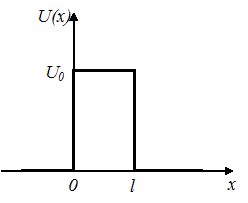
.

| квантовой частицы при 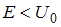 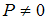 , а при , а при 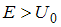 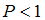 | ||
классической частицы при 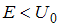 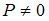 , а при , а при 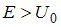 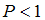 | |||
квантовой частицы при 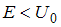 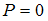 , а при , а при 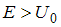 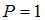 | |||
квантовой частицы 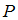 зависит только от зависит только от 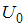 и не зависит от и не зависит от 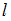 |
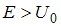 ), частица беспрепятственно проходит над барьером, то есть вероятность преодоления барьера
), частица беспрепятственно проходит над барьером, то есть вероятность преодоления барьера 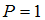 . Если же
. Если же 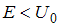 , то частица отражается от барьера, сквозь барьер она проникнуть не может и
, то частица отражается от барьера, сквозь барьер она проникнуть не может и 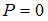 . Согласно квантовой механике даже при
. Согласно квантовой механике даже при 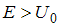 имеется отличная от нуля вероятность отражения частицы от барьера и, следовательно, вероятность преодоления барьера
имеется отличная от нуля вероятность отражения частицы от барьера и, следовательно, вероятность преодоления барьера 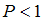 . При
. При 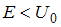 имеется отличная от нуля вероятность того, что частица проникнет сквозь барьер и окажется в области, где
имеется отличная от нуля вероятность того, что частица проникнет сквозь барьер и окажется в области, где 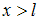 , то есть
, то есть 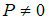 .
. ЗАДАНИЕ N 4
сообщить об ошибке
ЗАДАНИЕ N 4
сообщить об ошибке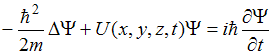 является утверждение, что оно …
является утверждение, что оно …

| является нестационарным | ||
| соответствует одномерному случаю | |||
| является стационарным | |||
| описывает состояние микрочастицы в одномерном бесконечно глубоком прямоугольном потенциальном ящике |
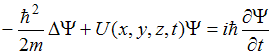 называют нестационарным (временным) уравнением Шредингера, так как функция
называют нестационарным (временным) уравнением Шредингера, так как функция 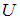 является функцией не только пространственных координат, но и времени, и оно содержит производную от функции
является функцией не только пространственных координат, но и времени, и оно содержит производную от функции 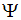 по времени.
по времени.