Преподаватель:
Специальность: 280101.65 - Безопасность жизнедеятельности в техносфере
Группа: ФЭН
Дисциплина: Физика
Идентификатор студента: 3
Логин: 01ps680461
Начало тестирования: 2012-03-07 14:28:33
Завершение тестирования: 2012-03-07 14:28:37
Продолжительность тестирования: 0 мин.
Заданий в тесте: 4
Кол-во правильно выполненных заданий: 0
Процент правильно выполненных заданий: 0 %
 ЗАДАНИЕ N 1
сообщить об ошибке
ЗАДАНИЕ N 1
сообщить об ошибке
Тема: Уравнения Шредингера (общие свойства)
Стационарное уравнение Шредингера в общем случае имеет вид 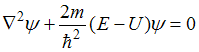 . Здесь
. Здесь 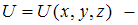 потенциальная
энергия микрочастицы. Электрону в одномерном потенциальном ящике с
бесконечно высокими стенками соответствует уравнение …
потенциальная
энергия микрочастицы. Электрону в одномерном потенциальном ящике с
бесконечно высокими стенками соответствует уравнение …
Решение:Для одномерного случая 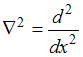 . Кроме того, внутри потенциального ящика U = 0,
а вне ящика частица находиться не может, так как его стенки бесконечно
высоки. Поэтому уравнение Шредингера для частицы в одномерном ящике с
бесконечно высокими стенками имеет вид
. Кроме того, внутри потенциального ящика U = 0,
а вне ящика частица находиться не может, так как его стенки бесконечно
высоки. Поэтому уравнение Шредингера для частицы в одномерном ящике с
бесконечно высокими стенками имеет вид 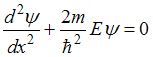 .
.
 ЗАДАНИЕ N 2
сообщить об ошибке
ЗАДАНИЕ N 2
сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
На рисунке дана схема
энергетических уровней атома водорода, а также условно изображены
переходы электрона с одного уровня на другой, сопровождающиеся
излучением кванта энергии. В ультрафиолетовой области спектра эти
переходы дают серию Лаймана, в видимой области – серию Бальмера, в
инфракрасной области – серию Пашена и т.д.
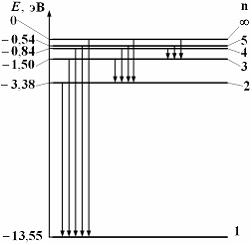
Отношение минимальной частоты линии в серии Бальмера 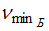 к максимальной частоте линии в серии Лаймана
к максимальной частоте линии в серии Лаймана 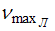 спектра атома водорода равно …
спектра атома водорода равно …
Решение:Серию
Лаймана дают переходы на первый энергетический уровень, серию Бальмера –
на второй уровень. Максимальная частота линии в серии Лаймана 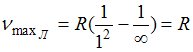 . Минимальная частота линии в серии Бальмера
. Минимальная частота линии в серии Бальмера 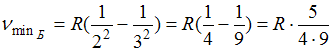 . Тогда
. Тогда 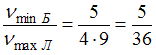 .
.
 ЗАДАНИЕ N 3
сообщить об ошибке
ЗАДАНИЕ N 3
сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
На рисунках схематически
представлены графики распределения плотности вероятности обнаружения
электрона по ширине одномерного потенциального ящика с бесконечно
высокими стенками для состояний с различными значениями главного
квантового числа n.
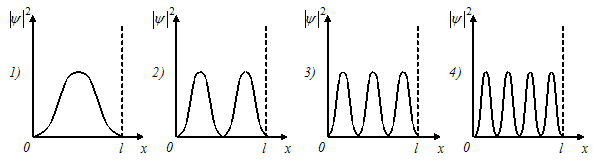
В состоянии с n = 3 вероятность обнаружить электрон в интервале от 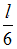 до
до 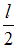 равна …
равна …
Решение:Вероятность обнаружить микрочастицу в интервале (a, b) для состояния, характеризуемого определенной 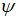 -функцией, равна
-функцией, равна 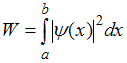 . Из графика зависимости
. Из графика зависимости 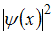 от х эта вероятность находится как отношение площади под кривой
от х эта вероятность находится как отношение площади под кривой 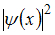 в интервале (a, b) к площади под кривой во всем интервале существования
в интервале (a, b) к площади под кривой во всем интервале существования 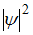 , то есть в интервале (0, l). При этом состояниям с различными значениями главного квантового числа n соответствуют разные кривые зависимости
, то есть в интервале (0, l). При этом состояниям с различными значениями главного квантового числа n соответствуют разные кривые зависимости 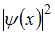 : n = 1 соответствует график под номером 1, n = 2 – график под номером 2 и т.д. Тогда в состоянии с
: n = 1 соответствует график под номером 1, n = 2 – график под номером 2 и т.д. Тогда в состоянии с 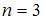 вероятность обнаружить электрон в интервале от
вероятность обнаружить электрон в интервале от 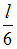 до
до 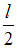 равна
равна 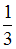 .
.
 ЗАДАНИЕ N 4
сообщить об ошибке
ЗАДАНИЕ N 4
сообщить об ошибке
Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
В опыте Дэвиссона и Джермера
исследовалась дифракция прошедших ускоряющее напряжение электронов на
монокристалле никеля. Если ускоряющее напряжение увеличить в 8 раз, то
длина волны де Бройля электрона _____ раз(-а).
Решение:Длина волны де Бройля 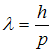 , где
, где 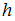 – постоянная Планка,
– постоянная Планка, 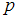 –
импульс частицы. При прохождении электроном ускоряющего напряжения
увеличивается его кинетическая энергия. Если считать начальную скорость
электрона равной нулю, то
–
импульс частицы. При прохождении электроном ускоряющего напряжения
увеличивается его кинетическая энергия. Если считать начальную скорость
электрона равной нулю, то 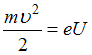 , где
, где 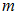 и
и 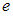 – масса и заряд электрона,
– масса и заряд электрона, 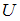 – ускоряющее напряжение,
– ускоряющее напряжение, 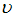 – приобретенная электроном скорость. После преобразований получим
– приобретенная электроном скорость. После преобразований получим 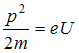 , или
, или 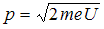 . Следовательно,
. Следовательно, 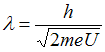 , и при увеличении ускоряющего напряжения
, и при увеличении ускоряющего напряжения 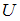 в 8 раз длина волны де Бройля электрона
в 8 раз длина волны де Бройля электрона 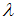 уменьшится в
уменьшится в 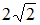 раз.
раз.

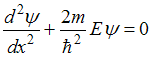
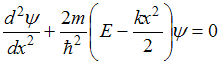
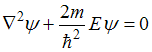
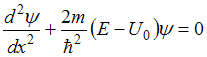
 ЗАДАНИЕ N 1
сообщить об ошибке
ЗАДАНИЕ N 1
сообщить об ошибке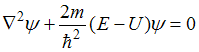 . Здесь
. Здесь 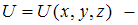 потенциальная
энергия микрочастицы. Электрону в одномерном потенциальном ящике с
бесконечно высокими стенками соответствует уравнение …
потенциальная
энергия микрочастицы. Электрону в одномерном потенциальном ящике с
бесконечно высокими стенками соответствует уравнение …
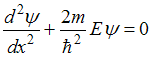
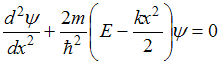
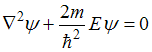
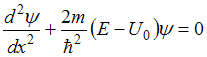
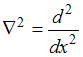 . Кроме того, внутри потенциального ящика U = 0,
а вне ящика частица находиться не может, так как его стенки бесконечно
высоки. Поэтому уравнение Шредингера для частицы в одномерном ящике с
бесконечно высокими стенками имеет вид
. Кроме того, внутри потенциального ящика U = 0,
а вне ящика частица находиться не может, так как его стенки бесконечно
высоки. Поэтому уравнение Шредингера для частицы в одномерном ящике с
бесконечно высокими стенками имеет вид 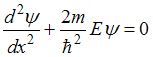 .
. ЗАДАНИЕ N 2
сообщить об ошибке
ЗАДАНИЕ N 2
сообщить об ошибке
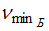 к максимальной частоте линии в серии Лаймана
к максимальной частоте линии в серии Лаймана 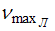 спектра атома водорода равно …
спектра атома водорода равно …
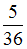
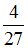
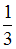
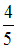
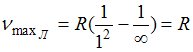 . Минимальная частота линии в серии Бальмера
. Минимальная частота линии в серии Бальмера 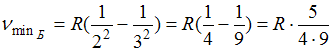 . Тогда
. Тогда 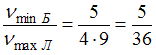 .
. ЗАДАНИЕ N 3
сообщить об ошибке
ЗАДАНИЕ N 3
сообщить об ошибке
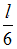 до
до 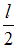 равна …
равна …
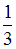
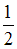
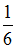
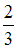
 -функцией, равна
-функцией, равна 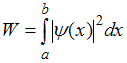 . Из графика зависимости
. Из графика зависимости 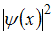 от х эта вероятность находится как отношение площади под кривой
от х эта вероятность находится как отношение площади под кривой 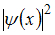 в интервале (a, b) к площади под кривой во всем интервале существования
в интервале (a, b) к площади под кривой во всем интервале существования 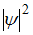 , то есть в интервале (0, l). При этом состояниям с различными значениями главного квантового числа n соответствуют разные кривые зависимости
, то есть в интервале (0, l). При этом состояниям с различными значениями главного квантового числа n соответствуют разные кривые зависимости 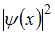 : n = 1 соответствует график под номером 1, n = 2 – график под номером 2 и т.д. Тогда в состоянии с
: n = 1 соответствует график под номером 1, n = 2 – график под номером 2 и т.д. Тогда в состоянии с 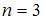 вероятность обнаружить электрон в интервале от
вероятность обнаружить электрон в интервале от 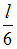 до
до 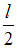 равна
равна 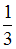 .
. ЗАДАНИЕ N 4
сообщить об ошибке
ЗАДАНИЕ N 4
сообщить об ошибке
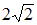
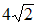
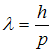 , где
, где 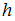 – постоянная Планка,
– постоянная Планка, 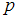 –
импульс частицы. При прохождении электроном ускоряющего напряжения
увеличивается его кинетическая энергия. Если считать начальную скорость
электрона равной нулю, то
–
импульс частицы. При прохождении электроном ускоряющего напряжения
увеличивается его кинетическая энергия. Если считать начальную скорость
электрона равной нулю, то 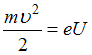 , где
, где 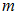 и
и 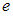 – масса и заряд электрона,
– масса и заряд электрона, 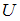 – ускоряющее напряжение,
– ускоряющее напряжение, 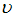 – приобретенная электроном скорость. После преобразований получим
– приобретенная электроном скорость. После преобразований получим 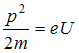 , или
, или 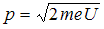 . Следовательно,
. Следовательно, 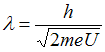 , и при увеличении ускоряющего напряжения
, и при увеличении ускоряющего напряжения 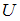 в 8 раз длина волны де Бройля электрона
в 8 раз длина волны де Бройля электрона 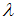 уменьшится в
уменьшится в 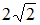 раз.
раз.