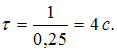Преподаватель:
Специальность: 280101.65 - Безопасность жизнедеятельности в техносфере
Группа: ФЭН
Дисциплина: Физика
Логин: 01ps680573
Начало тестирования: 2012-03-07 18:16:32
Завершение тестирования: 2012-03-07 18:16:36
Продолжительность тестирования: 0 мин.
Заданий в тесте: 4
Кол-во правильно выполненных заданий: 0
Процент правильно выполненных заданий: 0 %
 ЗАДАНИЕ N 1
сообщить об ошибке
ЗАДАНИЕ N 1
сообщить об ошибке
Тема: Волны. Уравнение волны
Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид 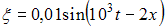 . Амплитуда ускорения колебаний частиц среды (в
. Амплитуда ускорения колебаний частиц среды (в 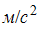 ) равна …
) равна …
Решение:Уравнение плоской синусоидальной волны имеет вид 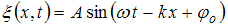 , где
, где 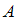 – амплитуда волны;
– амплитуда волны; 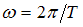 – циклическая частота;
– циклическая частота; 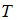 – период колебаний;
– период колебаний; 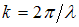 – волновое число;
– волновое число; 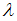 – длина волны; (
– длина волны; (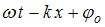 ) – фаза волны;
) – фаза волны; 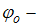 начальная фаза. Скорость колебаний частиц среды
начальная фаза. Скорость колебаний частиц среды 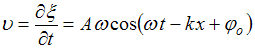 . Ускорение частиц среды
. Ускорение частиц среды 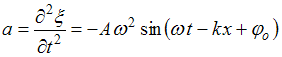 . Амплитуда ускорения частиц среды
. Амплитуда ускорения частиц среды 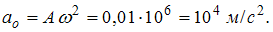
 ЗАДАНИЕ N 2
сообщить об ошибке
ЗАДАНИЕ N 2
сообщить об ошибке
Тема: Сложение гармонических колебаний
Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами 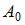 . Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
. Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
1. 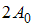
2. 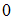
3. 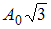
Решение:Амплитуда
результирующего колебания, полученного при сложении двух гармонических
колебаний одного направления с одинаковыми частотами, определяется по
формуле 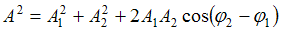 , где
, где 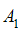 и
и 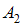 – амплитуды, (
– амплитуды, (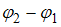 ) – разность фаз складываемых колебаний. Если амплитуда результирующего колебания
) – разность фаз складываемых колебаний. Если амплитуда результирующего колебания 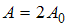 , то
, то 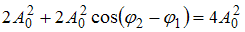 . Тогда
. Тогда 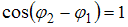 и разность фаз будет равна
и разность фаз будет равна 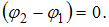
Если 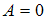 , то
, то 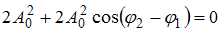 . Тогда
. Тогда 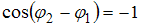 ; следовательно,
; следовательно, 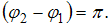
Если 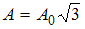 , то
, то 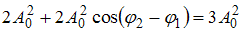 . Тогда
. Тогда 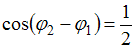 ; следовательно,
; следовательно, 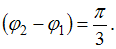
 ЗАДАНИЕ N 3
сообщить об ошибке
ЗАДАНИЕ N 3
сообщить об ошибке
Тема: Энергия волны. Перенос энергии волной
Если частоту упругой волны увеличить в 2 раза, не изменяя ее длины волны, то интенсивность волны увеличится в ___ раз(-а).
Решение:Интенсивностью
волны называется скалярная величина, равная модулю среднего значения
вектора плотности потока энергии (вектора Умова) 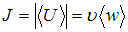 , где
, где 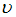 – скорость волны,
– скорость волны, 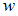 – объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением
– объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением 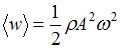 , где
, где 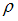 – плотность среды,
– плотность среды, 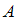 – амплитуда,
– амплитуда, 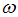 – циклическая частота волны. Тогда интенсивность волны равна
– циклическая частота волны. Тогда интенсивность волны равна 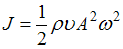 . Скорость волны
. Скорость волны 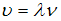 , где
, где 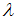 – длина волны,
– длина волны, 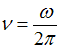 – ее частота. Таким образом,
– ее частота. Таким образом, 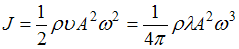 .
Следовательно, если частоту упругой волны увеличить в 2 раза, не
изменяя ее длины волны, то интенсивность волны увеличится в 8 раз.
.
Следовательно, если частоту упругой волны увеличить в 2 раза, не
изменяя ее длины волны, то интенсивность волны увеличится в 8 раз.
 ЗАДАНИЕ N 4
сообщить об ошибке
ЗАДАНИЕ N 4
сообщить об ошибке
Тема: Свободные и вынужденные колебания
Маятник совершает колебания, которые подчиняются дифференциальному уравнению 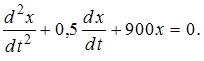 Время релаксации равно _____ c.
Время релаксации равно _____ c.
Решение:Дифференциальное уравнение затухающих колебаний имеет вид 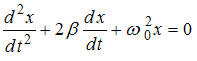 , где
, где 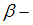 коэффициент затухания,
коэффициент затухания, 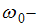 собственная круговая частота колебаний. Время релаксации
собственная круговая частота колебаний. Время релаксации 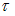 – это время, в течение которого амплитуда колебаний уменьшается в
– это время, в течение которого амплитуда колебаний уменьшается в 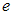 (~ 2,7) раз. Время релаксации связано с коэффициентом затухания:
(~ 2,7) раз. Время релаксации связано с коэффициентом затухания: 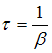 . Коэффициент затухания равен:
. Коэффициент затухания равен: 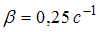 . Значит время релаксации
. Значит время релаксации 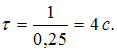

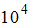
 ЗАДАНИЕ N 1
сообщить об ошибке
ЗАДАНИЕ N 1
сообщить об ошибке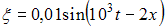 . Амплитуда ускорения колебаний частиц среды (в
. Амплитуда ускорения колебаний частиц среды (в 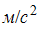 ) равна …
) равна …
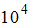
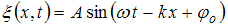 , где
, где 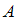 – амплитуда волны;
– амплитуда волны; 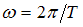 – циклическая частота;
– циклическая частота; 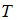 – период колебаний;
– период колебаний; 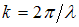 – волновое число;
– волновое число; 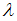 – длина волны; (
– длина волны; (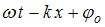 ) – фаза волны;
) – фаза волны; 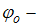 начальная фаза. Скорость колебаний частиц среды
начальная фаза. Скорость колебаний частиц среды 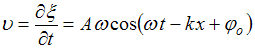 . Ускорение частиц среды
. Ускорение частиц среды 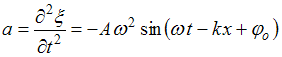 . Амплитуда ускорения частиц среды
. Амплитуда ускорения частиц среды 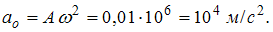
 ЗАДАНИЕ N 2
сообщить об ошибке
ЗАДАНИЕ N 2
сообщить об ошибке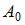 . Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
. Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.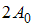
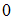
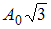
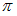
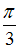
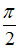
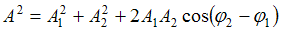 , где
, где 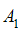 и
и 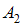 – амплитуды, (
– амплитуды, (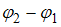 ) – разность фаз складываемых колебаний. Если амплитуда результирующего колебания
) – разность фаз складываемых колебаний. Если амплитуда результирующего колебания 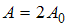 , то
, то 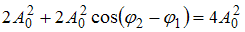 . Тогда
. Тогда 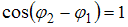 и разность фаз будет равна
и разность фаз будет равна 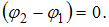
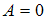 , то
, то 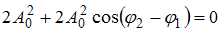 . Тогда
. Тогда 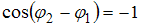 ; следовательно,
; следовательно, 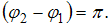
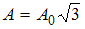 , то
, то 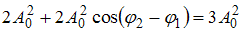 . Тогда
. Тогда 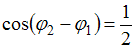 ; следовательно,
; следовательно, 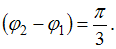
 ЗАДАНИЕ N 3
сообщить об ошибке
ЗАДАНИЕ N 3
сообщить об ошибке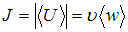 , где
, где 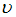 – скорость волны,
– скорость волны, 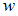 – объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением
– объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением 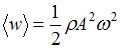 , где
, где 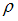 – плотность среды,
– плотность среды, 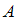 – амплитуда,
– амплитуда, 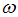 – циклическая частота волны. Тогда интенсивность волны равна
– циклическая частота волны. Тогда интенсивность волны равна 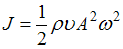 . Скорость волны
. Скорость волны 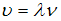 , где
, где 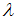 – длина волны,
– длина волны, 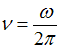 – ее частота. Таким образом,
– ее частота. Таким образом, 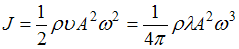 .
Следовательно, если частоту упругой волны увеличить в 2 раза, не
изменяя ее длины волны, то интенсивность волны увеличится в 8 раз.
.
Следовательно, если частоту упругой волны увеличить в 2 раза, не
изменяя ее длины волны, то интенсивность волны увеличится в 8 раз. ЗАДАНИЕ N 4
сообщить об ошибке
ЗАДАНИЕ N 4
сообщить об ошибке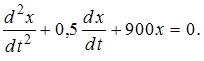 Время релаксации равно _____ c.
Время релаксации равно _____ c.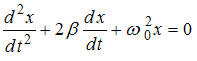 , где
, где 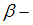 коэффициент затухания,
коэффициент затухания, 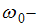 собственная круговая частота колебаний. Время релаксации
собственная круговая частота колебаний. Время релаксации 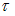 – это время, в течение которого амплитуда колебаний уменьшается в
– это время, в течение которого амплитуда колебаний уменьшается в 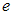 (~ 2,7) раз. Время релаксации связано с коэффициентом затухания:
(~ 2,7) раз. Время релаксации связано с коэффициентом затухания: 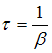 . Коэффициент затухания равен:
. Коэффициент затухания равен: 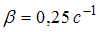 . Значит время релаксации
. Значит время релаксации